2024年4月20日，企业顶层设计专家(英国剑桥大学博士后)郑秀宝老师通过线上直播的形式为亚商同学主讲了《博弈论与决策》这门课程。郑老师以企业决策流程为切入点，阐述了博弈思维在决策中的用武之地。

　　

　　本堂课程主要围绕以下三个方面展开：

　　No.1

　　决策：博弈论的用武之地

　　No.2

　　博弈论的理论、方法与工具

　　No.3

　　系统思维与博弈论

　　博弈论的用武之地

　　老师开宗明义，直接点出了博弈论的用武之地——企业的商业决策。商业决策的具体哪个环节会需要博弈思维，答案就在下面。

　　企业商业决策的起点首先是找到问题，而产生问题的本质是因为事物的发展现状不及我们对其的期望。

　　

　　所以商业决策的第一步就是问题澄清。

　　所谓澄清问题，就是要把面对的“差距”描述清楚：“期望”是什么，“现状”是什么，两者相差几何?

　　

　　明晰问题之后，决策的第二步是分析结构。

　　为什么要分析结构，因为结构决定行为，行为决策绩效，因此不同的结构会导致不同的绩效。

　　

　　何为结构

　　两个要素彼此关联，形成一种关系。比如一个男孩一个女孩，彼此相爱，是谓恋爱关系;三个以上要素彼此关联，这种更为复杂的关系谓之结构，比如“三角恋”。

　　当明确了结构之后，接下来就是制定举措，解决问题。

　　在制定举措的时候，有三个要点需要决策层重视：

　　1

　　要点一

　　列出尽可能多的解决策略。

　　2

　　要点二

　　解决策略的评价标准必须明白清楚，特别是确认策略能否解决问题。

　　3

　　要点三

　　别把追求解答的手段当成解答本身。

　　博弈思维的用武之处便在商业决策的制定举措这一步骤中。

　　博弈论

　　博弈论是指双方或者多方在竞争、合作、冲突等情况下，充分了解各方信息，并依此选择能为本方争取最大利益的最优策略的理论。

　　

　　从博弈论的定义中可以看出，一场博弈必包涵三大要素：局中人、策略、得失。

　　依据不同的判断基准，会形成不同的博弈类型。

　　如下图所示：

　　

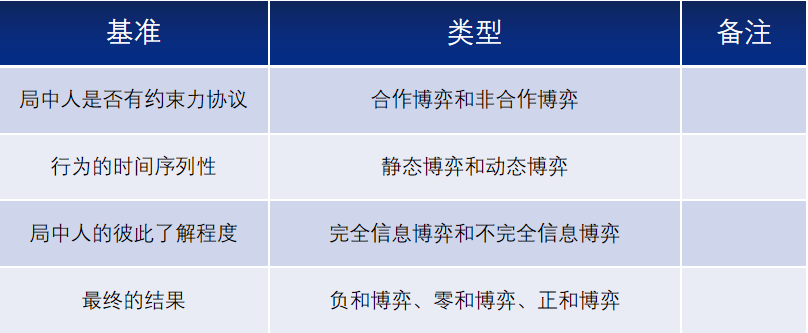
　　不管是什么类型的博弈，博弈的基本特点都是需要尽量考虑到博弈对方的决策选择及其对自己的影响，并从中选择出对自己最有利的决策方案，以此达到收益和效益最大化。

　　纳什均衡：最基本的博弈逻辑

　　

　　纳什均衡是由美国数学家约翰?福布斯?纳什最早提出，并由此获得诺贝尔经济学奖。纳什均衡研究的是非合作、完全信息且静态的博弈，是最基本的博弈模型，也是进一步博弈分析的基础。

　　在非合作、完全信息的静态博弈中，每个局中人都期望得到最大收益。如果一个局中人对对手的不同策略能找到同一个有利策略，这个策略叫他的占优策略。同样如果其他局中人也能找到自己的占优策略，那么一个所有局中人占优策略的组合，就是一个纳什均衡。

　　接着，老师通过解读博弈论的三大经典博弈模型，揭示了面对一场博弈，我们需要怎么来做。

　　这三大经典博弈模型分别是：囚徒困境、智猪博弈、美女游戏。

　　我们以“美女游戏”为例，为大家解读一下面对一场博弈，你应该做什么。

　　美女游戏背景

　　

　　一位陌生美女主动过来和你搭讪，并要求和你一起玩个游戏。美女提议:"让我们各自亮出硬币的一面，或正或反。如果我们都是正面，那么我给你3元，如果我们都是反面，我给你1元，剩下的情况你给我2元就可以了。"听起来不错的提议。如果我是男性，无论如何我是要玩的，不过经济学考虑就是另外一回事了，这个游戏真的够公平吗?

　　当你面临这一场博弈的时候，你首先要做的是把握结构，理清博弈中的关键要素。

　　

　　接下来第二步，我们要预测未来(将要发生的事情)。

　　我们首先要找到我们的占优策略，分析如下。

　　假设我们出正面的概率是x，反面的概率是1-x。为了使利益最大化，应该在对手出正面或反面的时候我们的收益都相等，不然对手总是可以改变正反面出现的概率让我们的总收入减少，由此列出方程就是3x+(-2)*(1-x)=(-2)*x+1*(1-x)。

　　上述方程通俗的说就是在对手一直出正面你得到的利益，和你对手一直出反面得到利益是一样的且最大。解方程得x=3/8,也就是说平均每八次出示3次正面，5次反面是我们的最优策略。而将x=3/8代入到收益表达式3*x+(-2)*(1-x)中就可得到每次的期望收入，计算结果是-1/8元。

　　接着我们站在美女的角度，找到对方的占优策略。

　　同样，设美女出正面的概率是y，反面的概率是1-y，列方程-3y+2(1-y)=2y+(-1)*(1-y)，解得y也等于3/8，而美女每次的期望收益则是2(1-y)-3y=1/8元。这告诉我们，在双方都采取最优策略的情况下，平均每次美女赢1/8元。

　　其实只要美女采取了(3/8,5/8)这个方案，不论你再采用什么方案，都是不能改变局面的。如果全部出正面，每次的期望收益是(3+3+3-2-2-2-2-2)/8=-1/8元;如果全部出反面，每次的期望收益也是(-2-2-2+1+1+1+1+1)/8=-1/8元。

　　经过上面的分析，你就会明白，面对这场博弈。只要美女采取她的占优策略，无论你怎么玩都是输。

　　当我们预测了未来要发生的事情之后，你要做的就是采取对策了。

　　那面对美女游戏这一场博弈，你会采取什么样的对策呢?

　　

　　博弈论的启示

　　亚当·斯密《国富论》中所谓的“看不见的手”，对“如何发展、繁荣市场经济”这一问题给出了答案。

　　但负和博弈模型告诉我们，如果市场中的每一个参与方都只追求各自的利益，结果有可能是给各方都带来不利。所以，可以肯定的是，的确存在“看不见的手”触及不到的领域。

　　系统思维

　　当我们面临一场博弈的时候，我们知道首先要做的第一件事是把握结构。但如果我们缺乏系统思维，往往我们是做不到把握结构的。

　　因为系统思维是一种把“认知”还原为“存在”的能力。

　　

　　上图所示，是用系统思维解决问题的路径图。当我们要想改变现状的时候，我们首先要去找到目前结构中包含的要素以及他们之间关系，然后去判断这种关系会导致什么样的结果，是否和我们想要的目标是一致的。

　　我们从下往上分析完问题之后，如果发现现存的结构无法达成我们想要的结构。那我们要做的首先是改变结构，改变系统中各个要素之间的关系，这样才能最终改变现状。

　　比如清末的康有为和梁启超这对师徒。一开始，两人的改革理念是一样的，认为想要改变清朝积贫积弱的现状，只需要进行制度改良就能做到。

　　后来戊戌变法失败之后，梁启超慢慢改变了自己的理念。认为只是制度改良并不能救中国，必须要推翻清朝的统治，重新构建社会制度才能强国富民。

　　而康有为还是坚持自己的改良理念，一条胡同走到黑，最终师徒两人分道扬镳。

　　END

　　哪些人适合读MBA?